Example 7.29: Bubble plots colored by a fourth variable

In Example 7.28, we generated a bubble plot showing the relationship among CESD, age, and number of drinks, for women. An anonymous commenter asked whether it would be possible to color the circles according to gender. In the comments, we showed simple code for this in R and hinted at a SAS solution for two colors. Here we show in detail what the SAS code would look like, and revisit the R code.


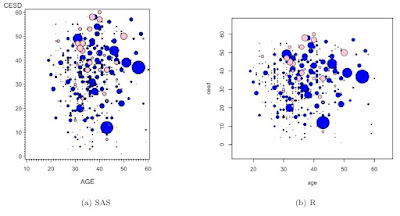
SAS

For SAS, we have to make two separate variables-- one with the CESD for the females, and another for the males. For the other gender, these gender-specific variables will have missing values. We'll do this using conditioning (section 1.11.2).

libname k "c:\book";

data twocolors;
set k.help;
  if female eq 1 then femalecesd = cesd;
  else malecesd = cesd;
run;

Now we can use the bubble2 statement (close kin of the plot2 statement, section 5.1.2) to add both gender-specific variables to the plot. While we're at it, we relabel the x-axis to no longer be gender specific and specify that the right y-axis is not to be labeled.

proc gplot data = twocolors;
bubble malecesd*age=i1 / bscale = radius bsize=200 
                           bcolor = blue bfill = solid;
bubble2 femalecesd*age=i1 / bscale = radius bsize = 200 
                           bcolor = pink bfill = solid noaxis;
label malecesd="CESD";
run;

As in the previous bubble plot example, the scale is manipulated arbitrarily so that the SAS and R figures are similar.

We're somewhat fortunate here that the range of the two gendered CESD scores are similar

R

In the comments for Example 7.28, we suggested the following simple R code.

load(url("http://www.math.smith.edu/sasr/datasets/savedfile"))
femalealc = subset(ds, female==1 & substance=="alcohol")
malealc = subset(ds, female==0 & substance=="alcohol")
with(malealc, symbols(age, cesd, circles=i1,
inches=1/5, bg="blue"))
with(femalealc, symbols(age, cesd, circles=i1,
inches=1/5, bg="pink", add=TRUE))

While this does generate a plot, it could be misleading, in that the scale of the circle sizes is relative to the largest value within each symbols() call. While this could be desirable, it's more likely that we'd like a single scale for the circles. R code for this can be made in a single statement:

load(url("http://www.math.smith.edu/sasr/datasets/savedfile"))
attach(ds)
symbols(age, cesd, circles=i1,inches=1/5, 
             bg=ifelse(female==1,"pink","blue")) 

Here the ifelse() function (section 1.11.2) generates a different circle fill color depending on the value of female.

The resulting plots are shown below.